Want to know how much work Christopher Nolan put into his movie, The Dark Knight Rises? Check out this official map of Nolan’s Gotham City from The Dark Knight Manual. It not only details key landmarks from the films, but also the surrounding area, rivers, the stadium…it’s all here. Click to enlarge.
What did you think of the map? What details did you notice?
[Via Reddit]

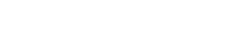

![Mapping the Dark Knight’s Gotham City [Movies]](https://i0.wp.com/www.thegeektwins.com/wp-content/uploads/2012/07/gotham-map-1.jpg?fit=600%2C318&ssl=1)


5 Comments
They put a lot more effort into that than I put into mine. http://www.ptdilloway.com/2012/03/your-guide-to-rampart-city.html
I noted the Central Park scene. I love that area.
One thing …make that two things, I didn't like about the movie:
1. Everybody and their mother is finding out that Bruce Wayne is Batman. Sucks!
2. Bane's voice is hard to understand at times. he's a bad knockoff of Darth Vader.
Cool maps, though. I just left NYC a week ago. It rocks!
By the way, if you're interested, I am hosting a 3-day blog fest called Dog Days of Summer from Aug 10-12. I'd love to have you aboard!
Cheers.
Considering the larger city scenes were filmed in Pittsburgh, I'm sure the map is similar to that city's layout. And smart choice to use Pittsburgh – with the 'Three Rivers,' there are a lot of bridges.
Neat map. Like all the little islands in it.
Well this kind of information is really worth searching for, good
information for readers and a value for you as will definitely show the quality
of the writer. It’s good to have these kinds of articles around to keep the
information flow steady. Helping those who really can make things right in the
future, good work!
buy
movies